

Georges Boole (1818-1864) met au point l'algèbre de Boole, basée sur l'utilisation du système binaire. Il démontre que tout processus logique peut être décomposé en une suite d’opérations logiques (et, ou, non) appliquées sur deux états (zéro-un, oui-non, vrai-faux, ouvert-fermé).
Ces opérateurs sont parfaitement définis par leur table de vérité :
| table du ET | table du OU | table du NON |
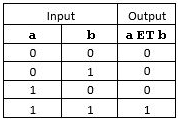 | 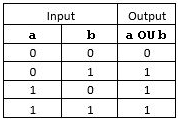 | 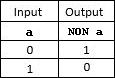 |
On peut aussi présenter les tables du ET, OU de la façon suivante :
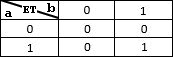 | 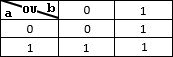 |
En utilisant exclusivement le "matériel" Python suivant :
def , if , else , == , returnEcrire 2 fonctions op_ET(a,b) , op_OU(a,b) permettant de retourner respectivement le résultat de (a ET b) et de (a OU b). |
|
#Code à copier dans votre éditeur et à compléter
def op_ET(a,b):
#Jeu d'essai
print("op_ET : pass test1 --> ",op_ET(0,0)==0)
print("op_ET : pass test2 --> ",op_ET(0,1)==0)
print("op_ET : pass test3 --> ",op_ET(1,0)==0)
print("op_ET : pass test4 --> ",op_ET(1,1)==1)
|
#Code à copier dans votre éditeur et à compléter
def op_OU(a,b):
#Jeu d'essai
print("op_OU : pass test1 --> ",op_OU(0,0)==0)
print("op_OU : pass test2 --> ",op_OU(0,1)==1)
print("op_OU : pass test3 --> ",op_OU(1,0)==1)
print("op_OU : pass test4 --> ",op_OU(1,1)==1)
|
Même s'il peut être défini à partir du ET et du OU l'opérateur XOU est à connaître car utiliser souvent.
| table du OU Exclusif |
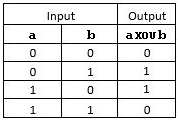 |
Voyons comment XOR peut-être défini à partir de ET,OU,NON.
En voici la démonstration via la table de vérité correspondante :
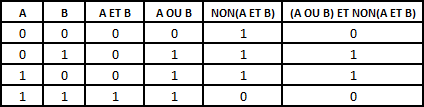 |
On peut assez facilement associer une expression booléenne à une table de vérité donnée.
Soit le nouvel opérateur op définit par sa table de vérité :
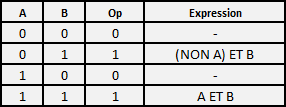
L'expression booléenne correspondant à notre nouvel opérateur est donc : op(a,b) = [(NON a) ET b] OU (a ET b).
A noter que l'algèbre binaire permetrait, comme on le fait en algèbre classique, de simplifier quand cela est possible une expression booléenne.