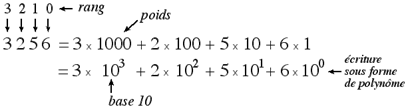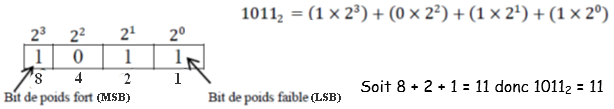Binaire & Nombres Entiers Naturels
Cet algorithme peut être mis en oeuvre au travers de l'activité Basic Machine.
Les ordinateurs codent l’information sous forme binaire. Nous allons voir ici, que ce code binaire correspond à un système de numération à base 2.
Ce point est important car il va permettre à l’ordinateur de faire des calculs sur l’information pour la traiter et la transformer.
La numération :
Dans toute numération, il faut distinguer chiffres et nombres.
- Un nombre est le résultat du comptage d'un ensemble d'objets, d'animaux, de personnes ...
- Pour écrire un nombre, on peut utiliser un ou plusieurs chiffres ( symboles ).
I-Numération décimale :
Dans la vie courante, nous pratiquons la numération décimale …reposant à l’origine sur nos dix doigts :
les dix symboles 0,1,2,3,4,5,6,7,8,9 (chiffres) permettent de représenter tous les nombres. (Base 10)
La position des chiffres est primordiale dans cette représentation (numération de position) :
il y a quelques années déjà, vous avez appris ce qu’étaient les unités (colonne de droite), les dizaines, les centaines, etc
On peut généraliser cette définition à une numération à base n :
- Si n = 2 alors on a le binaire : tout nombre est écrit avec 0 et 1.
- Si n = 16 alors on a l’hexadécimal : tout nombre s’écrit grâce à 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, et F
- Si n = 20 on a le vigésimal (cf. les mayas)
La place du chiffre dans le nombre a une signification. Il détermine la valeur ou le poids du chiffre.
Exemple : Décomposition du nombre 3256 :
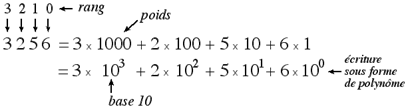
- On appelle le chiffre dont le poids est le plus élevé le « Most Significant Bit » ou MSB.
Ici, c’est le chiffre 3. Ce chiffre est toujours placé le plus à gauche du nombre.
- On appelle le chiffre dont le poids est le plus faible le « Least Significant Bit » ou LSB.
Ici, c’est le chiffre 6. Ce chiffre est toujours placé le plus à droite du nombre.
Chaque position a un poids fixe : 100 pour le rang 0 soit un poids de 1, 101 pour le rang 1 soit un poids de 10,
102 pour le rang 2 soit un poids de 100… C’est un code pondéré.
Ecrire une égalité semblable à celle donnée pour 3256 avec les puissances de 10 pour les nombres 2134 et 805.
II. La base 2 : le binaire
En base 2, pour représenter les nombres on utilise que 2 chiffres : 0 et 1 appelés bit ( binary digit).
Exemple : 1001
Chaque bit correspond à une puissance de 2, le plus à droite correspond à 2^0 , puis les exposants augmentent de 1 en remontant de la droite vers la gauche.
- Avec 1 bit, combien de nombres entiers naturels différents peut-on coder ? ...................................
- Avec 2 bits, combien de nombres entiers naturels différents peut-on coder ? ...................................
- Avec 3 bits, combien de nombres entiers naturels différents peut-on coder ? ...................................
- Avec 4 bits, combien de nombres entiers naturels différents peut-on coder ? ...................................
- Avec n bits, combien de nombres entiers naturels différents peut-on coder ? ...................................
Correspondance entre binaire et décimal :
Pour ne pas confondre les écritures, on écrira 1012 pour un nombre en base 2 et 101 pour un nombre en base 10.
a. Conversion d’un nombre binaire en base 10 :
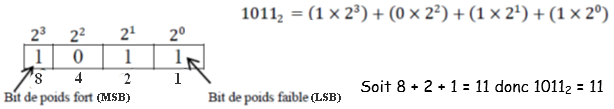
b. Conversion d’un nombre entier naturel en base 2 :
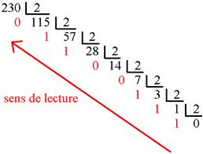
On effectue des divisions euclidiennes par 2, successives, et on s’arrête lorsque le quotient devient nul.
230 s’écrie donc en binaire 111001102
On peut aussi décomposer le nombre décimal à l’aide des puissances de 2 : 1, 2 ,4, 8, 16 , 32 , 64 , 128, 256
Convertissons 230 : 256 est plus grand que 230 donc on commence à 128
230 = 128 + 64 + 32 + 4 + 2 = 27+ 26+ 25+ 22+ 21= 1110 0110
Pour terminer
- Sur un octet, on peut représenter les nombres entiers naturels allant de 0 à : 1111 11112 =28 – 1 = 255
- Sur deux octets, on peut représenter les nombres entiers naturels allant de 0 à : 1111 1111 1111 11112 = 216 – 1 = 65 535
- Sur quatre octets, on peut représenter les nombres entiers allant de 0 à 232 – 1.
- Sur huit octets, c'est-à-dire 64 bits, on peut représenter tous les nombres entiers naturels allant de 0 à 264 - 1.
Exercices
Convertir en base 10 les nombres suivants : 11111111(2) ; 10010110(2)
Que se passe-t-il si on rajoute un 0 à droite d’un nombre binaire ?
Convertir en base 2 les nombres suivants 31 ; 109 ; 128 ; 253 ; 1000
A consulter :
- Informatique Lycée
Correction des Exercices
Question n°1
Convertir en base 10 les nombres suivants : 11111111(2) ; 10010110(2)
>>> Proposition de solution - Proposition de solution - Proposition de solution <<<
11111111(2) = 255(10)
10010110(2) = 150(10)
Question n°2
Que se passe-t-il si on rajoute un 0 à droite d’un nombre binaire ?
>>> Proposition de solution - Proposition de solution - Proposition de solution <<<
Cela revient à faire une multiplication par 2.
En effet, tout comme en base décimale un décalage à gauche représente une multiplication par 10, en base binaire,
un décalage à gauche correspond à une multiplication par 2. A contrario, le décalage à droite représente une division dans les mêmes proportions.
Question n°3
Convertir en base 2 les nombres suivants 31(10) ; 109(10) ; 128(10) ; 253(10) ; 1000(10)
>>> Proposition de solution - Proposition de solution - Proposition de solution <<<
31(10) = 11111(2)
109(10) = 1101101(2)
128(10) = 10000000(2)
253(10) = 11111101(2)
1000(10) = 1111101000(2)
