Tri par sélection

Principe de l’algorithme

Le tri par sélection se décompose en deux étapes :

• Sélectionner un élément (d'où son nom).
• Le placer à sa bonne place.

Le facteur qui détermine si un élément est bien placé est son rang (par exemple : le ième plus petit élément sera forcément placé en ième position du tableau). Le tri par sélection va donc à chaque tour trouver le ième plus petit élément du tableau, pour ensuite l'insérer à sa place, en commençant par le premier plus petit, et en augmentant à chaque fois (deuxième plus petit, troisième, etc.).

Exemple

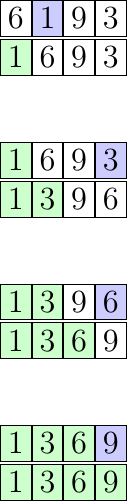
Prenons désormais comme exemple la suite de nombres suivante : 6, 1, 9, 3. Trions cette suite avec l’algorithme du tri par sélection dans l’ordre croissant :

1er tour :

6, 1, 9, 3 -> le plus petit élément du tableau est 1, on le place donc sur la première case (en l'échangeant avec le 6).

2ème tour :

1, 6, 9, 3 -> le deuxième plus petit élément est 3, on le place sur la deuxième case et on l’échange avec le 6.

3ème tour :

1, 3, 9, 6 -> le troisième plus petit élément est 6, on l’échange avec 9 pour le placer sur la troisième case.

4ème tour :

1, 3, 6, 9 -> le quatrième plus petit élément du tableau est 9, il est déjà en quatrième position on ne fait rien.

1, 3, 6, 9

Ce tri se décompose réellement en deux étapes distinctes :

À chaque tour, on cherche le minimum dans l'espace non trié du tableau (le minimum est représenté en bleu, et la partie non triée en blanc), ensuite on déplace cet élément à sa place définitive (représentée en vert). En faisant cela pour chaque élément du tableau, ce dernier se retrouve trié au bout de $N$ tours maximum ($N$ étant la taille du tableau).

Pseudo-code

Le pseudo-code du tri par sélection est simple :

triSelection :

   Pour chaque élément
      Pour chaque élément de la partie non triée
         Mettre à jour le minimum du tableau rencontré jusqu'ici
      Échanger l'élément actuel avec le minimum

Complexité

Le tri par sélection a une complexité en $O(N^2)$ :

• La première boucle parcourt $N$ tours.
• La deuxième boucle parcourt $N – i$ tours ($i$ variant de 0 à $N$).

Sa complexité est donc légèrement inférieure à $N^2$, cependant cette différence est mineure et sa complexité est considérée comme étant en $O(N^2)$.

Conclusion

Le tri par sélection est donc un algorithme assez simple, mais peu efficace à cause de sa complexité en $O(N^2)$. Cependant des améliorations et des variantes permettent de le rendre plus rapide, et le tri par sélection sert de base à d'autres algorithmes plus efficaces que nous étudierons plus tard.