Tri par insertion

Introduction

Le tri par insertion (insertion sort en anglais) est un algorithme de tri par comparaison simple, et intuitif mais toujours avec une complexité en $O(N^2)$. Vous l’avez sans doute déjà utilisé sans même vous en rendre compte : lorsque vous triez des cartes par exemple. C’est un algorithme de tri stable, en place, et le plus rapide en pratique sur une entrée de petite taille.

Principe de l’algorithme

Le principe du tri par insertion est de trier les éléments du tableau comme avec des cartes :

• On prend nos cartes mélangées dans notre main.
• On crée deux ensembles de carte, l’un correspond à l’ensemble de carte triée, l’autre contient l’ensemble des cartes restantes (non triées).
• On prend au fur et à mesure, une carte dans l’ensemble non trié et on l’insère à sa bonne place dans l’ensemble de carte triée.
• On répète cette opération tant qu’il y a des cartes dans l’ensemble non trié.

Exemple

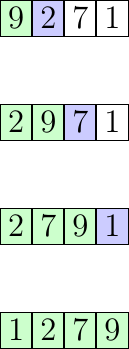
Prenons comme exemple la suite de nombre suivante : 9, 2, 7, 1 que l’on veut trier en ordre croissant avec l’algorithme du tri par insertion :

1er tour :

9 | 2, 7, 1 -> à gauche la partie triée du tableau (le premier élément est considéré comme trié puisqu'il est seul dans cette partie), à droite la partie non triée. On prend le premier élément de la partie non triée, 2, et on l'insère à sa place dans la partie triée, c'est-à-dire à gauche de 9.

2ème tour :

2, 9 | 7, 1 -> on prend 7, et on le place entre 2 et 9 dans la partie triée.

3ème tour :

2, 7, 9 | 1 -> on continue avec 1 que l’on place au début de la première partie.

1, 2, 7, 9

Pour insérer un élément dans la partie triée, on parcourt de droite à gauche tant que l'élément est plus grand que celui que l'on souhaite insérer.

Pour résumer l'idée de l'algorithme :

La partie verte du tableau est la partie triée, l'élément en bleu est le prochain élément non trié à placer et la partie blanche est la partie non triée.

Pseudo-code

triInsertion :

   Pour chaque élément non trié du tableau
      Décaler vers la droite dans la partie triée, les éléments supérieurs à 
      celui que l'on souhaite insérer
      Placer notre élément à sa place dans le trou ainsi créé

Complexité

L’algorithme du tri par insertion a une complexité de $O(N^2)$ :

• La première boucle parcourt $N – 1$ tours, ici on notera plutôt $N$ tours car le $– 1$ n’est pas très important.
• Décaler les éléments de la partie triée prend $i$ tours (avec $i$ variant de 0 à $N$).

Dans le pire des cas on parcourt $N^2$ tours, donc le tri par insertion a une complexité en temps de $O(N^2)$.

Conclusion

L'algorithme du tri par insertion est simple et relativement intuitif, même s'il a une complexité en temps quadratique. Cet algorithme de tri reste très utilisé à cause de ses facultés à s'exécuter en temps quasi linéaire sur des entrées déjà triées, et de manière très efficace sur de petites entrées en général.