Le tri par sélection

Il consiste à trouver dans le tableau le numéro de l'élément le plus petit, c'est-à-dire l'entier min tel que tab[k] >= tab[min] pour tout k. Une fois ce numéro trouvé, les éléments tab[1] et tab[min] sont échangés - cet échange nécessite une variable temporaire de type entier - puis la même procédure est appliquée sur la suite d'éléments tab[2], ..., tab[N].

/* Procédure de tri par sélection */ 

procedure triSelection(entier[] tab) 
   entier i, k; 
   entier min; 
   entier tmp; 
   pour (i de 1 à N-1 en incrémentant de 1) faire 
      /* recherche du numéro du minimum */ 
      min <- i; 
      pour (k de i+1 à N en incrémentant de 1) faire 
         si (tab[k] < tab[min]) alors 
           min <- k; 
         fin si 
      fin pour 
      /* échange des valeurs entre la case courante et le minimum */ 
      tmp <- tab[i]; 
      tab[i] <- tab[min]; 
      tab[min] <- tmp; 
   fin pour 
fin procedure 

Il est facile de compter le nombre d'opérations. Quel que soit l'ordre du tableau initial, le nombre de comparaisons reste le même, ainsi que le nombre d'échanges. À chaque itération, on considère l'élément tab[i] et on le compare successivement à tab[i+1], ..., tab[N]. On fait donc N-i comparaisons.

Le nombre total de comparaisons est donc de :

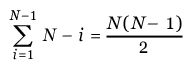et il y a (N-1) échanges.

En ce qui concerne sa complexité, on dit que le tri par sélection est en O (N²), à la fois dans le meilleur des cas, en moyenne et dans le pire des cas, c'est-à-dire que son temps d'exécution est de l'ordre du carré du nombre d'éléments à trier.