Le tri par insertion

Cette méthode de tri est très différente de la méthode de tri par sélection et s'apparente à celle utilisée pour trier ses cartes dans un jeu : on prend une carte, tab[1], puis la deuxième, tab[2], que l'on place en fonction de la première, ensuite la troisième tab[3] que l'on insère à sa place en fonction des deux premières et ainsi de suite. Le principe général est donc de considérer que les (i-1) premières cartes, tab[1],..., tab[i-1] sont triées et de placer la i^e carte, tab[i], à sa place parmi les (i-1) déjà triées, et ce jusqu'à ce que i = N.

Pour placer tab[i], on utilise une variable intermédiaire tmp pour conserver sa valeur qu'on compare successivement à chaque élément tab[i-1],tab[i-2],... qu'on déplace vers la droite tant que sa valeur est supérieure à celle de tmp. On affecte alors à l'emplacement dans le tableau laissé libre par ce décalage la valeur de tmp.

/* Procédure de tri par insertion */ 
procedure triInsertion(entier[] tab) 
   entier i, k; 
   entier tmp; 
   pour (i de 2 à N en incrémentant de 1) faire 
      tmp <- tab[i]; 
      k <- i; 
      tant que (k > 1 et tab[k - 1] > tmp) faire 
         tab[k] <- tab[k - 1]; 
         k <- k - 1; 
      fin tant que 
   tab[k] <- tmp; 
   fin pour 
fin procedure 

La comparaison avec les deux algorithmes précédents montre que la complexité du tri par insertion est plus fortement dépendante de l'ordre du tableau initial. Nous comptons ici le nombre de comparaisons (qui est le nombre de décalages à un près) :

• dans le meilleur des cas, le tableau initial est trié et on effectue alors une comparaison à chaque insertion, on effectue donc N-1 comparaisons ;
• en moyenne, on montre que le nombre de comparaisons est de :

  ;

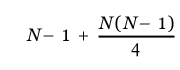
• dans le pire des cas, les entiers du tableau sont initialement donnés dans l'ordre décroissant. Dans ce cas, on effectue l'échange à chaque comparaison, c'est-à-dire que le nombre d'échanges est alors de :

  .

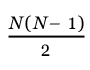
Contrairement aux tris par sélection et bulle qui nécessitent un nombre constant de comparaisons, le tri par insertion ne conduit qu'à très peu de comparaisons lorsque le tableau initial est presque en ordre. Ce tri a donc de meilleures propriétés.