Algorithme des k voisins les plus proches
(KNN)
(KNN)
Cet algorithme peut être mis en oeuvre au travers de l'activité patisserie.
L'algorithme des K plus proches voisins (KNN - k Nearest Neighbors) est un algorithme d'apprentissage automatique supervisé simple et facile à mettre en œuvre.
Un algorithme d'apprentissage automatique supervisé (par opposition à un algorithme d'apprentissage automatique non supervisé) est un algorithme qui repose sur des données d'entrée étiquetées qui permettent de définir une fonction par apprentissage, fonction qui va fournir une réponse appropriée lorsque de nouvelles données non étiquetées sont fournies.
Un algorithme d’apprentissage automatique non supervisé utilise des données d’entrée sans étiquette. Contrairement à l'apprentissage supervisé qui essaie d'apprendre une fonction qui nous permettra de faire des prédictions à l'aide de nouvelles données non étiquetées, l'apprentissage non supervisé essaie d'apprendre de la structure des données pour nous donner plus d'informations sur celle-ci.
Imaginez qu’un ordinateur soit un enfant, nous voulons que l’enfant apprenne à quoi ressemble une fleur.
Pour cela, nous allons lui montrer plusieurs images différentes, en lui indiquant lesquelles sont des fleurs et lesquelles ne le sont pas !
Quand on voit une fleur, on crie «fleur !"» Quand ce n'est pas une fleur, on crie «pas fleur !».
Cela correspond à un apprentissage automatique supervisé.
Après cette phase d'apprentissage l'enfant doit normalement être capable si on lui montre une photo de fleur de dire "fleur !"
Prenons l'exemple de la reconnaissance de la langue d'un texte (Français ou Anglais) à partir de l'analyse des fréquences des lettres utilisées.
Dans un soucis de simplification, nous ne prendrons en considération que les lettres U et H qui sont suffisamment discriminantes pour distinguer ces 2 langues.
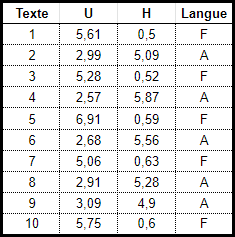
Le tableau ci-dessous indique pour plusieurs textes écrits en Anglais ou en Français la fréquence d'apparition des lettres "U" et "H".
Comme dans notre exemple, un problème de classification a une valeur discrète en sortie, c'est à dire un résultat "binaire" (Tout ou Rien, O ou 1, 2 ou 3). Il n'y a pas de valeurs intermédiaires possibles. Par exemple, “Français” et “Anglais” sont discrets. Il n'y a pas de juste milieu. Notre exemple d'identification d'une fleur par un enfant est un autre exemple de problème de classification ("Fleur" ou "pas Fleur").
Revenons sur notre reconnaissance de la langue, nous avons 2 prédicteurs (fréquence de la lettre U et fréquence de la lettre "H") et une étiquette (F : Français ou A : Anglais)).
Il est courant de représenter la sortie (étiquette) d’un algorithme de classification sous la forme d’un nombre entier tel que 1, -1 ou 0. Dans notre exemple, cela pourrait-être (1) pour Français et (0) pour Anglais. Dans ce cas, ces nombres sont purement représentatifs. Les opérations mathématiques ne doivent pas être effectuées sur eux, car cela n'aurait aucun sens. Pensez un instant : "Qu'est-ce que la somme 1 + 0 pourrait bien représenter dans notre exemple". Nous ne pouvons pas ajouter ces valeurs.
Un problème de régression a quand à lui en sortie une valeur numérique réelle (1; 3,5; 7,2). Par exemple, le tableau ci-dessous permet d'estimer l'age d'un crabe (étiquette de valeur décimale) en fonction de sa largeur et de sa masse (prédicteurs).
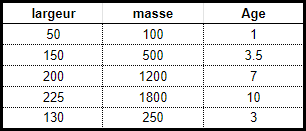
Les données utilisées dans une analyse de régression seront similaires aux données présentées ci-dessus.
Les descripteurs sont des variables indépendantes alors que l'étiquette est une variable dépendante. Dans notre exemple l'age du crabe dépend de sa largeur et de sa masse.
Notons à ce propos, que la largeur et la masse sont indépendantes car elles varient également en fonction du sexe de l'animal.
Reprenons notre exemple de reconnaissance de la langue dans un texte.
Pour chaque donnée du tableau on dispose d'un couple de prédicteurs (fréquence "U",fréquence "H") auquel on peut associer un point dans un repère.
On va donc pouvoir positionner les différentes données dans cet espace (repère dans ce cas - 2 prédicteurs).
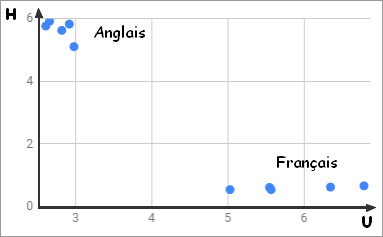
L'algorithme KNN suppose que des objets similaires existent à proximité dans cet espace (plus proches voisins). En d'autres termes, des choses similaires sont proches les unes des autres. Cette notion de proximité peut-être formaliser par un calcul de distance entre des points du graphique. La distance la plus courament utilisée est la distance Euclidienne (il en existe d'autres : distance Manhattan, distance Hamming, ...).
Etant donné un nouveau texte dont on souhaite deviner la langue en fonction de la fréquence d'apparition de la lettre U et de la lettre H, appelons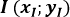 
le point du repère associé à ce texte inconnu !
Etant donné un texte connu de notre base d'apprentissage, appelons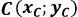 
le point du repère associé à ce texte.
Nous pouvons calculer la distance entre notre texte inconnu et notre texte connu grâce à la formule :
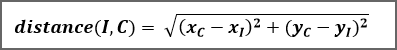
Il faut calculer cette distance entre le point I et tous les points Cj de notre base d'appentissage. Puis sélectionner les k plus proches voisins de I. La valeur de k étant à définir (généralement entre 3 et 5).
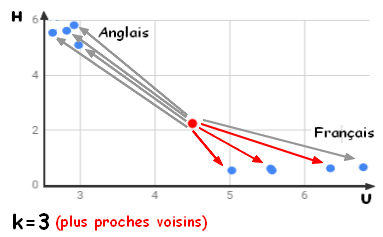
Reste à définir l'étiquette de notre inconnu.
Voilà, nous avons maintenant toutes les informations utiles pour décrire plus en détail le principe de l'agorithme :
Algorithme KNN (base apprentissage, k, inconnu)
- Pour chaque donnée dans la base d'apprentissage
- Calculez la distance entre l'inconnu et la donnée courante.
- Mémoriser cette distance et la donnée associée dans une liste de couple (distance, donnée).
- Triez la liste distance_Donnée du plus petit au plus grand sur les distances.
- Choisissez les k premières entrées de cette liste.
- Obtenir les étiquettes des k données de la base d'apprentissage sélectionnées.
- Si régression, renvoyer la moyenne des étiquettes K.
- Si classification, renvoyer l'étiquette majoritaire.
Pour sélectionner le K qui convient à nos données, nous pouvons exécuter plusieurs fois l'algorithme KNN avec différentes valeurs de K et choisir le K qui réduit le nombre d'erreurs rencontrées tout en maintenant la capacité de l'algorithme à effectuer des prédictions avec précision.
Lorsque nous diminuons la valeur de K à 1, nos prévisions deviennent moins stables. En effet, dans le cas de notre reconnaissance de la langue d'un texte, si le point I est entouré d'un majorité de point de type "F:Français", et que le plus proche est un point de type "A:Anglais", l'algorithme va conclure qu'il s'agit d'un texte en Anglais alors qu'il est en Français. Inversement, à mesure que nous augmentons la valeur de K, nos prévisions deviennent plus stables en raison du vote à la majorité. Puis K augmentant nous commençons à être témoin d'un nombre croissant d'erreurs. C’est à ce stade que nous savons que nous avons poussé la valeur de K trop loin. Notez que dans les cas de classification où choisissons l'étiquette majoritaire, la valeur de K doit être un nombre impair pour avoir un départage entre les étiquettes.
Dans le cas où notre étude comporte n prédicteurs, soit n coordonnées, on utilise un espace à n dimensions.
Pour la reconnaissance on peut retenir 26 prédicteurs (les fréquences des 26 lettres de l'alphabet). On travail alors dans un espace de dimension 26 !
Les coordonnées d'un point sont alors notées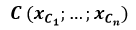 
.
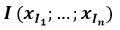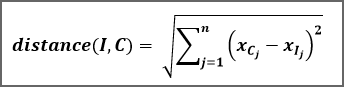
Cette liste est loin d'être exhaustive.
L'algorithme naïf de recherche de voisinage consiste à passer sur l'ensemble des n points de A et à regarder si ce point est plus proche ou non qu'un des plus proches voisins déjà sélectionné, et si oui, l'insérer. On obtient alors un temps de calcul linéaire en la taille de A : O(n) (tant que k << n). Cette méthode est appelée la recherche séquentielle ou recherche linéaire.
L'algorithme kN-voisin (KNN) est un algorithme d'apprentissage automatique supervisé simple qui peut être utilisé pour résoudre des problèmes de classification et de régression. Il est facile à mettre en œuvre et à comprendre, mais présente l’inconvénient majeur de ralentir considérablement à mesure que la taille des données utilisées augmente.
KNN recherche les distances entre une "inconnu" et toutes les données de la base d'apprentissage, sélectionne le nombre spécifié exemples (K) les plus proches de la requête, puis vote pour l'étiquette la plus fréquente (dans le cas de la classification) ou pour la moyenne des étiquettes (en le cas de la régression).
Dans le cas de la classification et de la régression, nous avons vu que choisir le bon K pour nos données se faisait en essayant plusieurs K et en choisissant celui qui fonctionnait le mieux.