Je teste mes connaissances :
Algorithme Knn
Algorithme Knn
Question n°1
Voici un arbre, on le parcourt en partant du haut (la racine) et en descendant de branche en branche (les noeuds) jusqu'à arriver à une feuille.
Par exemple on peut faire le parcourt Racine 4 puis noeud 5 puis noeud 4 puis feuille 6.
Considérons un algorithme Glouton de parcours de cet arbre, Séletionnant le noeud le plus grand à chaque étape.
Quel chemin cet algorithme Glouton va-t-il parcourir ?
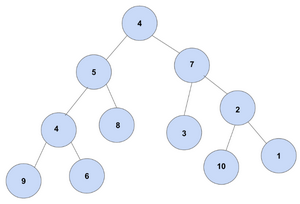
Il s'agit du chemin Racine 4, puis Noeud 7 puis feuille 3 (4-->7-->3).
Question n°2
On considère le problème où l’on doit rendre la monnaie pour 8 euros avec le moins possible de pièces de monnaies.
On dispose de pièces de 1,4,6 euros.
Donner le rendu de monnaie donné par un algorithme glouton.
Cette solution est-elle optimale ?
L’algorithme glouton n’est pas optimal pour le jeu de pièces de valeurs (6, 4, 1) : pour x = 8, le glouton renvoie 8 = 6 + 1 + 1 alors que la solution optimale est 8 = 4 + 4.
Question n°3
On considère le problème où l’on doit rendre la monnaie pour x euros avec le moins possible de pièces de monnaies.
On dispose de pièces de 1, 2, 5, 10 euros.
Donner un sous-ensemble de pièces (parmi 1, 2, 5, 10) tel que l’algorithme glouton ne trouve pas de solution pour x = 6.
L’algorithme glouton ne trouve pas de solution pour le jeu de pièces de valeurs (5, 2) : pour x = 6.