

Un algorithme glouton (on dit aussi gourmand) est un algorithme simple et intuitif utilisé dans les problèmes où l'on recherche une solution optimale (problèmes d'optimisation).
Prenons l'exemple ci-dessous correspondant à un problème d'optimisation :
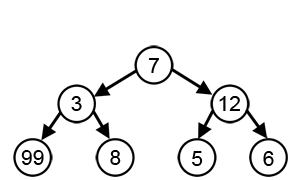
Il s'agit de trouver un chemin partant de la racine de l'arbre et dont la somme des étiquettes est la plus grande possible.
La solution optimale est indiquée ici en vert.
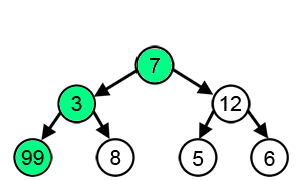
Un algorithme Glouton fait un choix optimal à chaque étape avec l'idée de trouver la solution optimale pour résoudre le problème dans son ensemble.
Dans le cas de la recherche de notre chemin dans un arbre, l'algorithme glouton sélectionne le plus grand nombre disponible à chaque étape.
Notons que le terme anglais "greedy" se traduit également par cupide, avide, qui illustre bien l'idée de cet algorithme qui est de choisir la grande valeur possible à chaque étape.
Cependant, comme nous pouvons le voir dans l'animation ci-dessous, cette approche ne parvient toujours pas à trouver la somme la plus élevée, En effet l'algorithme prend des décisions uniquement en fonction des informations dont il dispose à chaque étape, sans tenir compte du problème global.
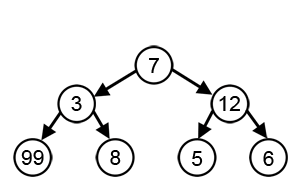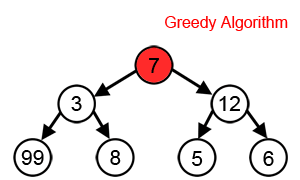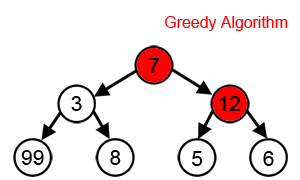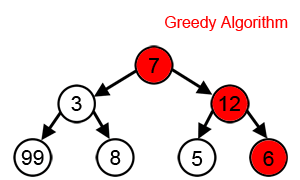
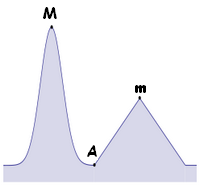
Dans le deuxième exemple ci-dessous, l'objectif est de trouver la valeur maximum de la courbe. La mise en oeuvre d'une solution à l'aide d'un algorithme Glouton, consiste, en partant du point A à chercher à monter selon la plus forte pente. Avec cette approche on trouve le maximum local m, mais pas le maximum global M.
Notons, que les algorithmes Gloutons réussissent assez bien dans certains problèmes, tels que l' encodage de Huffman, utilisé pour compresser les données, ou l'algorithme de Dijkstra , qui permet de trouver le chemin le plus court dans un graphe.
Quoiqu'il en soit, même si la stratégie gourmande ne produit pas toujours une solution optimale, elle permet de proposer une solution.
C'est le cas par exemple dans le problème dit "du sac à dos" et dans le problème dit "du rendu de monnaie" que nous allons détailler ci-dessous.

Pour info, le problème du sac à dos est l'un des 21 problèmes NP-complets de Richard Karp, exposés dans un article de 1972. La formulation du problème est fort simple, mais sa résolution est plus complexe.

Le problème consiste à remplir un sac à dos, ne pouvant supporter plus d'une certaine masse, avec tout ou partie d'un ensemble donné d'objets ayant chacun une masse et une valeur. Les objets mis dans le sac à dos doivent maximiser la valeur totale, sans dépasser la masse maximum.

Une astuce consiste à trier les objets dans l'ordre décroissant de leur valeur.
masse : Liste des masses respectives de ces objets dans cet ordre.
valeur : Liste des valeurs respectives de ces objets dans cet ordre.
objets_sac : liste des numéro d'objets choisis.
masse_charge := 0 : Masse totale des objets mis dans le sac à dos.
masse_maxi : Charge maximale admise dans le sac à dos
n : le nombre d'objets disponibles.
pour i de 1 à n
si masse[i] + masse_charge ≤ masse_maxi alors
ajouter à objets_sac indice i
masse_charge <- masse_charge + masse[i]
fin si
fin pour
objets_sac : contient la liste des indices des objets choisis.
remarque:
Plutôt que de trier les objets par valeurs décroissantes, on peut aussi travailler avec le ratio valeur/Masse.
Si les objets sont déjà triés par ordre décroissant de valeur, alors la boucle bornée de 1 à n correspond à une complexité de l'ordre de O(n).
Par contre si la liste des objets n'est pas triée on passe à une compléxité de l'ordre de O(n logn).
Le problème du rendu de monnaie s'énonce de la façon suivante : étant donné un système de monnaie (pièces et billets), comment rendre une somme donnée de façon optimale, c'est-à-dire avec le nombre minimal de pièces et billets ?
L'approche "gloutonne" de notre algorithme revient à considérer les pièces une par une, en commençant par les pièces de plus grande valeur, et de décroître le montant à rendre (en enlevant la valeur de la pièce que l’on considère à ce moment) jusqu’à ce que le montant soit inférieur à la valeur de la pièce que l’on regarde. On considère alors la plus grande valeur de pièce inférieure au montant, et on itère le raisonnement jusqu’à ce que le montant atteigne zéro.
Par exemple, ma machine veut rendre 1 euro 22 centimes.
Si nous avons à notre disposition des pièces de : 1 euro, 50 centimes, 10 centimes, 2 centimes , 1 centimes.
Le principe de notre algorithme est le suivant :
Au final, l’algorithme retourne “rendre 1 pièce de 1 euro, 2 pièces de 10 centimes, 1 pièce de 2 centimes”.

Une astuce consiste à trier les pièces dans l'ordre décroissant de leur valeur.
fonction moneyback(amount,coins)
chosen = [0,0,0,0,0] : effectif des pièces utilisées
Pour i allant de 1 à n
Tant que amount >= coins[i]
amount <- amount - coins[i]
chosen[i] <- chosen[i] + 1
Retourner le tableau chosen
Exemple d'exécution :
amount = 177 coins = [100,50,10,5,2] moneyback(amount, coins) >> chosen = [1, 1, 2, 1, 1]
Si les objets sont déjà triés par ordre décroissant de valeur, alors :
D'où une complexité de l'ordre de O(n).
Par contre si la liste des objets n'est pas triée on passe à une compléxité de l'ordre de O(n logn).

Si on considère l'affranchissement du courrier avec des timbres de valeurs :
1, 10, 21, 34, 70, 100.
Supposons que nous devions affranchir une lettre à 140 cents.
Notre algorithme donnerait : 140¢ = 100 + 34 + 1 + 1 + 1 + 1 + 1 + 1.
Alors que la solution optimale en nombre de timbres est : 140¢ = 70 + 70.

sources : (voir ressources ci-dessus)