Recherche dichotomique.

Présentation

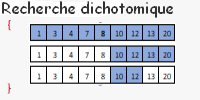
Supposons que le problème posé soit de trouver un nom dans un annuaire téléphonique qui consiste en une liste triée alphabétiquement.

On peut s'y prendre de plusieurs façons différentes. En voici deux :

• Rechercher linéaire : rechercher la personne en parcourant tous les noms en partant du début de l'annuaire.
• Recherche dichotomique : ouvrir l'annuaire au milieu, si le nom qui s'y trouve est plus loin alphabétiquement que le nom cherché, regarder avant, sinon, regarder après. Refaire l'opération qui consiste à couper les demi-annuaires (puis les quarts d'annuaires, puis les huitièmes d'annuaires, etc.) jusqu'à trouver le nom cherché.

Algorithme itératif.

L'algorithme ci-dessous recherche une valeur dans un tableau de nombres.

rechercheDichotomique(t,val) {
   // t : liste de n valeurs                                       
   // recherche dans t[0],...,t[n]
   a=0
   b=n
   TantQue (a<=b) {
     m = entier((a+b)/2)
     Si (t[m]==val) {
       retourner m;
     } Sinon Si(t[m]<val) {
       b = m-1;
     } else {
       a = m+1;
     }
   }
   retourner  Null
}

Algorithme récursif.

La version récursive de cet algorithme :

rechercheDichotomique(t,val,a,b) {
    // t : liste de n valeurs                                       
    // recherche dans t[a],...,t[b]
    Si(a<=b) {
      m = entier((a+b)/2);
      Si (t[m]==val) {
        retouner m;
      } Sinon Si (t[m] < val) {
        retourner rechercheDichotomique(t,val, a, m-1);
      } Sinon {
        return rechercheDichotomique(t,val,, m+1, b);
      }
    } Sinon {
      retourner null;
    }
  }

Appel de la fonction avec par exemple : rechercheDichotomique(t,12,0,n)

Complexité algorithmique.

L'algorithme de recherche dichotomique demandera dans le pire des cas de séparer en deux l'annuaire, puis de séparer à nouveau cette sous-partie en deux, ainsi de suite jusqu'à n'avoir qu'un seul nom. Supposons que le nombre de références de l'annuaire soitn. Le nombre d'étapes nécessaires sera le nombre entier qui est immédiatement plus grand que log₂(n), par exemple, si n vaut 30 000, le nombre d'itérations est 15 (car 2¹⁵ vaut 32 768).

La complexité (le nombre d'opérations) de ce second algorithme dans le pire des cas est alors log₂(n), ce qui veut dire que l'ordre de grandeur du nombre d'opérations de ce pire cas est le logarithme en base 2 de la taille de l'annuaire, c'est-à-dire que pour un annuaire dont la taille est comprise entre 2^p-1 et 2^p, il sera de l'ordre de p. On peut écrire aussi bien O(ln(n)) ou O(log₂(n)) car ln(n) et log₂(n) ont le même ordre de grandeur.

Ressources :